Теоретическое обоснование способов измерения крупногабаритных тел вращения
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ СПОСОБОВ ИЗМЕРЕНИЯ КРУПНОГАБАРИТНЫХ ТЕЛ ВРАЩЕНИЯ
При ремонте крупногабаритных изделий таких как бандажи цементных печей одним из наиболее актуальных вопросов является вопрос, связанный с получением информации о реальной форме изношенного бандажа. Задача усложняется тем, что деталь в процессе работы имеет нестационарную ось вращения. В этой связи наиболее предпочтительным является создание виртуальной модели бандажа по результатам измерения его геометрических параметров.
В результате анализа исследований можно допустить, что искажение формы бандажа происходит в большинстве случаев в двух более или менее выраженных направлениях. Данное положение позволяет допустить, что сечение бандажа по образующей определяется замкнутым контуром с положительной кривизной, в некоторых случаях приближающимся к форме эллипса.
Все это позволяет высказать гипотезу о возможности аппроксимировать контур бандажа дугами окружностей с определенным радиусом. Данный подход дает возможность с достаточной точностью определить замкнутый контур с положительной кривизной при условии правильного подбора длин дуг окружностей, аппроксимирующих реальный контур.
Представим контур бандажа в виде выпуклой замкнутой кривой, образованной плавно состыкованными в узловых точках окружностями. Эти окружности последовательно проходят через три точки с шагом, равным одному узлу. Для проведения теоретических расчетов контур бандажа в одном из сечений удобно представить кривой Безье с положительной кривизной.
Проведем геометрическое обоснование рассматриваемого способа на примерах различных контуров.
На рисунке 2.1 (а) показана аппроксимация дугами окружностей контура эллиптической формы, при условии, что каждая начальная точка последующей дуги совпадает с конечной точкой предыдущей дуги.
Назовем данный метод аппроксимацией дугами без перекрытия.
а) б)
б)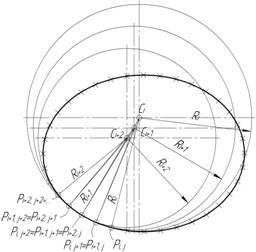
Рис. 2.1. Аппроксимация контура эллипса дугами окружностей:
а) при последовательном сопряжении дуг.
б) при сопряжении дуг с перекрытием.
На рисунке 2.1 (б) показана аппроксимация дугами окружностей контура эллиптической формы, при условии, что каждая начальная точка последующей дуги совпадает со средней точкой предыдущей дуги, а каждая средняя точка последующей дуги совпадает с конечной точкой предыдущей дуги. Назовем данный способ аппроксимацией дугами с перекрытием.
Из проведенного геометрического анализа, выполненного с использованием параметрической САПР КОМПАС-3D V7, можно судить о наличии математической закономерности в расположении центров аппроксимирующих окружностей. Поэтому оба метода в равной степени могут быть применены для проведения измерений.
Однако, необходимо заметить, что реальный контур бандажа не возможно представить в виде правильного эллипса. Более того, на поверхности могут наблюдаться локальные дефекты, которые в последствии могут влиять на формообразования и изменять форму бандажа совершенно неопределенным образом. В связи с этим необходимо провести геометрический анализ при аппроксимации замкнутого контура произвольной формы с положительной кривизной.
На рис. 2.2. приведен пример геометрической интерпретации аппроксимации дугами окружностей произвольно заданного замкнутого контура. Аналогично предыдущим положениям – при аппроксимации контура эллиптической формы, – проведем геометрический анализ при двух способах:
–методом аппроксимации дугами окружностей без перекрытия (рис 2.2 а);
– методом аппроксимации дугами окружностей c перекрытием (рис. 2.2. б).
Существенным является то, что центры аппроксимирующих дуг окружностей лежат произвольным образом, и в неопределенном порядке.
