Диффузионный факел образуется при раздельной подаче топлива и воздуха, так что горение зависит в основном от условий их смешения. Известно, что в топках паровых котлов и во вращающихся печах интенсифицируют процесс смешения, придавая воздуху или топливу начальную закрутку. Но влияние начальной закрутки на параметры факела и теплотехнологические процессы изучено еще не достаточно.

Исследование процессов диффузионного горения и теплоотдачи факела возможно методами математического моделирования процессов, так как оно позволяет изучать поля скорости, давления, температуры и концентраций веществ в факеле. Математическая модель состоит из системы дифференциальных уравнений в частных производных и граничных условий. Для вращающихся потоков топлива и воздуха требуется в общем случае решение сложной трехмерной задачи.

В данной работе рассматривается возможность учета закрутки компонентов горения в более простой двумерной постановке задачи, когда, например, рассматривая процессы в топке жаротрубного парового котлов или во вращающейся печи, пренебрегают наличием слоя технологического материала и влиянием выталкивающей силы.

В общем случае система дифференциальных уравнений движения, кроме уравнения неразрывности, содержит три уравнения Навье–Стокса. Запишем их в цилиндрических координатах x, r, j для стационарной задачи без учета силы тяжести в соответствии с [1]:

,

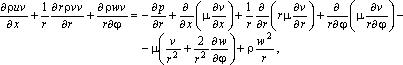
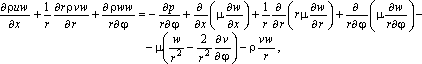где r – плотность; u, v и w – компоненты скорости по осям x, r и j соответственно; m – динамический коэффициент вязкости; p – давление;

При математической формулировке двумерной задачи задается положение точки по длине х и по радиусу r в цилиндрической системе координат. Физические величины вследствие осевой симметрии остаются постоянными по углу j, так что все производные по координате j обращаются в нуль. Чтобы учесть при этом вращение потоков топлива, воздуха и продуктов горения, нужно сохранить дифференциальное урав­нение для окружной скорости w, считая ее скалярной величиной. В результате уравнения Навье–Стокса приобретают следующий вид:

,

,

.

Последнее слагаемое во втором уравнении представляет собой центробежную силу, посредством которой в основном и учитывается влияние окружной скорости w на движение газа.

Закон сохранения массы, примененный к стационарному движению сплошной среды, приводит к дифференциальному уравнению неразрывности потока для двумерной задачи в цилиндрических координатах:

В математической модели это уравнение преобразуется в дискретное уравнение для расчета давления.

Дифференциальные уравнения движения дополняются в основном граничными условиями 1-го рода. На входе задается скорость, на выходе более удобно задавать давление, что позволяет приближенно рассчитать скорость в выходном сечении. На входе производная от давления по оси x считается равной нулю (граничные условия 2-го рода). На стенках продольная и поперечная компоненты скорости газа равны нулю из условия "прилипания" потока, а давление на стенке исключается из уравнений принятым построением сетки. На оси потока всегда задаются граничные условия 2-го рода.