Расчет сталебетонных плит с односторонним армированием
РАСЧЕТ СТАЛЕБЕТОННЫХ ПЛИТ С ОДНОСТОРОННИМ
АРМИРОВАНИЕМ
Внешняя арматура в виде листов или прокатных профилей позволяет конструировать экономически эффективные сталебетонные плиты при ограниченных размерах сечений. К расчету сталебетонной плиты с металлическим листом применима модель ![]() двухслойной плиты с поперечной неоднородностью. Поперечные связи можно считать абсолютно жесткими [1].
двухслойной плиты с поперечной неоднородностью. Поперечные связи можно считать абсолютно жесткими [1].

Рис.1 Элементы сталебетонной плиты с несимметричной поперечной неоднородностью
Рассмотрим сталебетонную плиту, показанную на рис. 1. Толщина слоя стали – hs, толщина слоя бетона – hb. Введем физические константы, характеризующие оба слоя: модули продольной упругости Es и Eb, температурные коэффициенты линейной деформации ![]() и
и ![]() коэффициенты теплопроводности
коэффициенты теплопроводности ![]() и
и![]() .
.
В целях упрощения расчетов принимаем коэффициенты Пуассона ![]() не изменяющимся по толщине плиты. В данном случае это оправдывается небольшой разницей его значений для стали и бетона.
не изменяющимся по толщине плиты. В данном случае это оправдывается небольшой разницей его значений для стали и бетона.
Поперечная нагрузка на поверхности плиты имеет интенсивность, а температурное поле задано функцией
T(x, y, z)=T0(x, y) + ![]() T(x, y)*f(z), (1)
T(x, y)*f(z), (1)
где T0(x, y) – средняя величина температур нижней и верхней поверхностей; ![]() T(x, y) – разница между температурами тех же поверхностей; f(z) – функция, зависящая от теплопроводности материалов [2]:
T(x, y) – разница между температурами тех же поверхностей; f(z) – функция, зависящая от теплопроводности материалов [2]:
 (2)
(2)
При Es > Eb нейтральный слой смещается вдоль оси Z на величину e в положительном направлении. Для ее определения используем условие равенства нулю продольной силы вдоль оси x(y). При использовании гипотезы прямых нормалей условие ![]() представляется в виде уравнения [3]
представляется в виде уравнения [3]
 . (3)
. (3)
Таким образом,
 . (4)
. (4)
В рассматриваемом частном случае
![]() . (5)
. (5)
Цилиндрическая жесткость в общем случае имеет вид
 (6)
(6)
В рассматриваемом частном случае
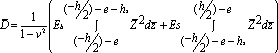 . (7)
. (7)
Таким образом,
 (8)
(8)
Эта формула легко проверяется с помощью зависимости между моментами инерции относительно параллельных осей и исправляет формулу(5.82) в книге [2].
Напряжения при изгибе плиты от температурного поля можно получить, умножив правую часть (1) на температурный коэффициент линейной деформации ![]() . Эти напряжения вносят свой вклад в выражения внутренних усилий, так что дифференциальное уравнение плиты с несимметричной поперечной неоднородностью получаем в следующем виде:
. Эти напряжения вносят свой вклад в выражения внутренних усилий, так что дифференциальное уравнение плиты с несимметричной поперечной неоднородностью получаем в следующем виде: