Рассмотрим пример реализации генетического алгоритма на примере следующей задачи: даны десять карт, пронумерованных от 1 до 10, необходимо разделить их на две стопки так, чтобы сумма значений карт первой стопки была как можно ближе к 36, а произведение значений карт второй как можно ближе к 360. Эта задача является классическим примером задачи поиска оптимального значения.

Сначала необходимо породить начальную популяцию. В качестве отдельной особи можно взять одномерный массив из 10 элементов, случайным образом заполненный числами от 1 до 10, так чтобы в нем не было повторяющихся чисел. Эта особь после процесса эволюционирования и будет решением, произведение первых n чисел которой должно быть максимально близко к 360, а сумма остальных максимально близка к 36, где n не является четко заданным числом. (Следует заметить, что такое распределение (сначала произведение, затем сумма) имеет лучшую сходимость, чем обратное, поскольку при увеличении длины последовательности складываемых и умножаемых чисел, сумма в процентном соотношении изменяется гораздо медленнее произведения).

После порождения начальной популяции необходимо подсчитать коэффициент выживаемости каждой особи. В качестве коэффициента выживаемости можно выбрать сумму относительных погрешностей суммы и произведения, т.е. сумму отклонений произведения от 360 и суммы от 36.

После порождения начальной популяции и подсчета ее коэффициента выживаемости начинается цикл эволюции. Он подразделяется на три основные операции: подсчет вероятностей стать родителем для особей популяции (селекция или отбор), порождение новой популяции (скрещивание и мутация), и пересчет коэффициентов выживаемости особей с проверкой условия выхода из цикла (которым является либо удельный коэффициент выживаемости – т.е. найдена особь точно соответствующая решению задачи, либо достижение порогового значения числа итераций цикла эволюции). Завершение цикла эволюции по условию достижения порогового значения числа итераций означает, что точное решение задачи не было найдено. Для генетического алгоритма это является вполне нормальной ситуацией. К этому могут привести много факторов непостоянных от задачи к задаче. Примерами таких факторов служат, например, неверный выбор критерия выживаемости, малая размерность начальной популяции, и, конечно же, малое пороговое значение числа итераций цикла эволюции. Увеличение размерности начальной популяции, и порогового значения числа итераций цикла эволюции почти всегда приводит к улучшению сходимости задачи, но тут следует помнить и о разумности и достаточности, ведь увеличение этих характеристик приводит к заметному увеличению времени счета задачи. К примеру, оптимальными для данной задачи можно выбрать размерность начальной популяции 100 и пороговое значение итераций 500. Ниже (на рис. 2, 3 и 4) представлены графики результата работы программы в зависимости от размерности начальной популяции и порогового значения цикла эволюции. Увеличение расстояния между значением коэффициента выживаемости (фитнеса) решения и среднего значения коэффициента выживаемости последней популяции означает увеличение числа точных решений. Т.о. видно, что увеличение размерности популяции приводит к увеличению вероятности отыскания точного решения, а увеличение порогового значения итераций цикла эволюции к улучшению (приближению к желаемому результату) всей популяции.

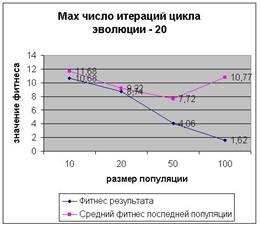
Рисунок 2.

Рисунок 3.